トップページ
 研究活動
研究活動
 研究チーム紹介
研究チーム紹介
 過去の研究チーム紹介
過去の研究チーム紹介
 平尾計算化学研究ユニット
平尾計算化学研究ユニット
平尾計算化学研究ユニット
English
ユニットリーダー 平尾 公彦
(ひらお きみひこ)研究概要
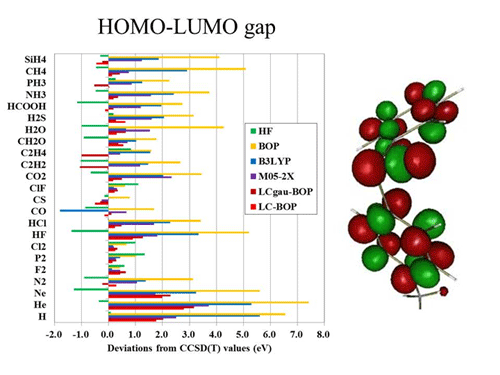
現在、分子科学でもっともよく使われている理論は密度汎関数法(DFT)法である。計算が比較的簡単であること、定量性があること、そして計算結果の解釈が容易であることがその理由である。しかしDFT法は理論的に解決しなければならないさまざまな問題を抱えている。ポテンシャル面(遷移状態)の記述に問題があるし、励起状態の記述にも改善の余地がある。van der Waals力などの弱い相互作用の記述は難しい。これらの欠陥はいずれも長距離での電子密度の記述の悪さに起因している。われわれは誤差関数を利用して、2電子反発積分を短距離積分と長距離積分に分離し、短距離にはDFTの汎関数を利用し、長距離にはHartree-Fock法の積分を利用する新しい汎関数(LC)を開発した。このLC汎関数を時間依存DFT法と組み合わせることでRydberg励起や電荷移動の励起状態の定量的計算が可能になった。またDFTではこれまで記述できなかったvan der Waals相互作用を定量的できるようになり、分極率の定量的評価も可能となった。LCはDFTの適用範囲を大幅に拡張したといっても過言ではない。最近、LC-DFTがHartree-Fock法と同じようにKoopmans定理を満足することを証明した。平尾計算化学研究ユニットでは理論をさらに発展させ、LCを汎関数の決定版として確立する。またLC-DFTの計算から化学反応の制御や分子設計を行う。同時に「京」のアーキテクチャーに適した並列化アルゴリズム開発やオーダーN化を実現し、生体分子やナノマテリアルのような現実系にも応用する予定である。