アクセス
Facebook
X
Instagram
YouTube
日本語
お問い合わせ
トップページ
研究活動
研究チーム紹介
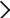大規模並列数値計算技術研究チーム
大規模並列数値計算技術研究チーム
English
チームプリンシパル 今村 俊幸
（いまむら としゆき）
imamura.toshiyuki[at]riken.jp （拠点：神戸）- Emailの[at]は@にご変更ください。
- 1996
- 京都大学大学院工学研究科応用システム
- 科学専攻単位取得退学
- 1996
- 日本原子力研究所計算科学技術推進センター
- 並列処理基本システム開発グループ
- 2000
- 博士（工学）取得
- 2002
- ドイツ・シュツッツガルト大学HLRS
- Guest Scientist
- 2003
- 電気通信大学講師・助教授（2007 より准教授）
- 2012
- AICS 大規模並列数値計算技術研究チーム チームリーダー（現職）
キーワード
- 並列数値アルゴリズム
- 高性能計算
- 数値線形代数
- 混合精度数値計算
- 最低限精度計算法
研究概要
研究チームでは、スーパーコンピュータ「富岳」上での大規模・高並列・高性能な数値計算ソフトウェアライブラリの研究開発を推進します。シミュレーションプログラム開発には、連立一次方程式や固有値計算、高速フーリエ変換、非線形方程式など様々な数値計算アルゴリズムが欠かすことでできませんが、「富岳」の能力を最大限に利用するには、「高並列」「高性能」「高精度」「耐障害性」「大規模化」といった観点からアルゴリズムを選定しライブラリとして整備する必要があります。これらの研究は、計算科学（シミュレーション）、計算機科学（ハードウェア、ソフトウェア）と応用数学などの強固な連携によって達成されます。R-CCSにおける強固な協力体制のもとに次世代の高性能計算システムも視野に入れた数値計算ライブラリKMATHLIBにおける基盤技術の確立を進めたいと考えています。
主な研究成果
世界最高速の固有値計算に成功
行列の固有値計算は、大規模なコンピュータシミュレーションや、ビッグデータにおけるデータ相関関係の解析などで必ず使用されますが、その計算量が行列の次元の3 乗に比例して増加し、計算時間がかかるために大規模問題を高速に計算することが難しいのです。従来の計算アルゴリズムでは、（1）密行列を三重対角行列に変換する前処理を行い、（2）その後に、三重対角行列の固有値計算を行って固有ベクトルを得、（3）最後に、もとの行列の固有ベクトルにします（図の緑線部分）が、計算が大規模になると（1）に膨大な時間がかかります。この問題への解決方法として、前処理として一度、帯行列に変換し、さらに三重対角行列に変換する2段階のスキーム（図の青線部分）も開発されましたが、前処理部分を高速化できるものの、後処理部分の計算量が2倍以上に増加してしまいます。EigenExa は、帯行列を直接導くことで、この流れを効率化する新たなスキーム（図の赤線部分）に基づくソフトウェアであり、「京」の全プロセッサを用いることで、100万×100万の行列の固有値問題を1 時間以内で解くことができました。過去の我々が知る世界最大規模の固有値計算は、地球シミュレータ（初代）の4992プロセッサを用いて40万×40万行列を3 時間半で解いた記録でした。
Traditional 1-step scheme
主要論文
- Yuki Uchino, Toshiyuki Imamura.:
"High-Performance EigenSolver Combining EigenExa and Iterative Refinement"
SC '24: Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, 2024 - Takeshi Terao, Toshiyuki Imamura, and Katsuhisa Ozaki.:
"Iterative refinement for an eigenpair subset of a real symmetric matrix"
JSIAM Letters, Vol. 16, pp. 89-92, 2024, doi: 10.14495/jsiaml.16.89 - Piotr Luszczek, Ahmad Abdelfattah, Hartwig Anzt, Atsushi Suzuki, Stanimire Tomov.:
"Batched sparse and mixed-precision linear algebra interface for efficient use of GPU hardware accelerators in scientific applications"
Future Generation Computer Systems-The International Journal of Science, Vol.160, pp. 359-374, 2024, doi: 10.1016/j.future.2024.06.004 - Yuta Hasegawa, Naoyuki Onodera, Yuuichi Asahi, Takuya Ina, Toshiyuki Imamura, and Yasuhiro Idomura.:
"Continuous data assimilation of large eddy simulation by lattice Boltzmann method and local ensemble transform Kalman filter (LBM-LETKF)"
Fluid Dynamics Research, Vol. 55, Number 6, 2023, doi: 10.1088/1873-7005/ad06bd - Daichi Mukunoki, Satoshi Kawai, and Toshiyuki Imamura.:
"Sparse Matrix-Vector Multiplication with Reduced-Precision Memory Accessor"
2023 IEEE 16th International Symposium on Embedded Multicore/Many-core Systems-on-Chip (MCSoC), pp. 608-615, 2023. doi: 10.1109/MCSoC60832.2023.00094 - Atsushi Suzuki.:
"A factorization algorithm for sparse matrix with mixed precision arithmetic"
ECCOMAS Congress 2022, Volume Science Computing, 2022. doi 10.23967/eccomas.2022.006 - Hisashi Yashiro, Koji Terasaki, Yuta Kawai, Shuhei Kudo, Takemasa Miyoshi, Toshiyuki Imamura, Kazuo Minami, Hikaru Inoue, Tatsuo Nishiki, Takayuki Saji, Masaki Satoh, and Hirofumi Tomita.:
"A 1024-member ensemble data assimilation with 3.5-km mesh global weather simulations"
Proc. The International Conference for High Performance Computing, Networking, Storage and Analysis (SC '20). IEEE Press, Article 1, 1–10, 2020. doi: 10.1109/SC41405.2020.00005 - Daichi Mukunoki, Katsuhisa Ozaki, Takeshi Ogita, Toshiyuki Imamura.:
"DGEMM using Tensor Cores, and Its Accurate and Reproducible Versions"
ISC High Performance 2020, Lecture Notes in Computer Science, Vol.12151, pp. 230-248, 2020. doi.org/10.1007/978-3-030-50743-5_12 - Takeshi Fukaya and Toshiyuki Imamura.:
"Performance evaluation of the EigenExa eigensolver on Oakleaf-FX: tridiagonalization versus pentadiagonalization"
Proc. Parallel and Distributed Processing Symposium Workshop (IPDPSW), 2015 IEEE International, pp. 960-969, 2015. doi: 10.1109/IPDPSW.2015.128 - Yusuke Hirota and Toshiyuki Imamura.:
"Divide-and-Conquer Method for Banded Generalized Eigenvalue Problems"
Journal of Information Processing Computing System, Vol.52,Nov,20,2015.
