トップページ
 計算科学研究センターとは
計算科学研究センターとは
 人材育成
人材育成
 計算科学eラーニング
計算科学eラーニング
 データ同化
データ同化
 International Symposium/School on Data Assimilation
International Symposium/School on Data Assimilation
 International Symposium on Data Assimilation-Online (ISDA-Online)
International Symposium on Data Assimilation-Online (ISDA-Online)
 "Space-Time Multigrid for the Maximum Likelihood Ensemble Filter Method"
"Space-Time Multigrid for the Maximum Likelihood Ensemble Filter Method"
"Space-Time Multigrid for the Maximum Likelihood Ensemble Filter Method"
The International Symposium on Data Assimilation Online (ISDA-Online) 8 Jan,2021 "Data Assimilation Methodology"
International Symposium on Data Assimilation - Online![]()
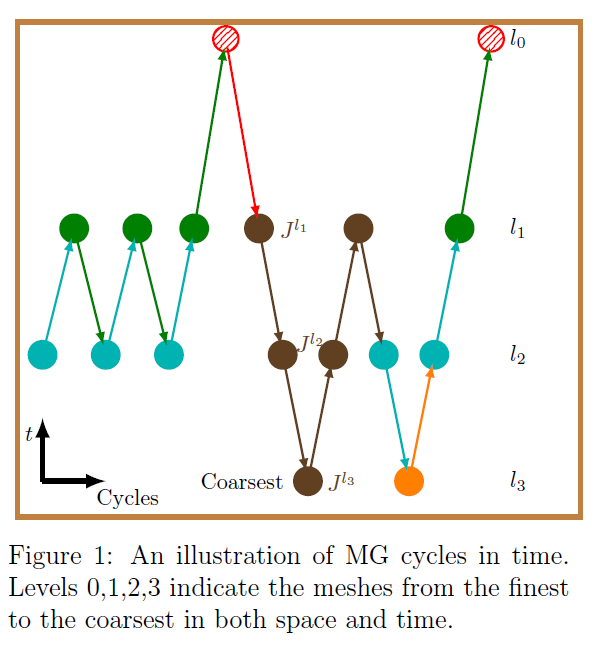
In this work, we propose a new method to improve the computational efficiency of minimizing a 4D-variational-ensemble optimal control system. The new method employs multigrid in space and time to aim for model reduction by successively restricting the full system to lower resolutions for more efficient assimilation, while incorporating the covariance information during the multigrid process to ensure the essential dynamical properties are retained and predicted with sufficient accuracy. This work is motivated by applying data assimilation to high dimensional nonlinear engineering applications such as turbulent combustion. While the meteorological community already employs spatial multigrid methods with data assimilation, applying multi-grid reduction in time (MGRIT) to data assimilation is new. Using MGRIT, parallel in time can provide further speedups and effectively make use of future architecture. The 4D-variational-ensemble assimilation method is based on the maximum likelihood ensemble filter (MLEF). The cost function is derived based on a Gaussian probability density function framework and Bayes theorem. While the original MLEF is an ensemble-based sequential data assimilation method, we herein introduce the assimilation of data over a time window, a summation of multiple time terms instead of a single time term in the original MLEF, which adds the ingredient of strong constraint 4D-variational assimilation. The core concept is achieved by solving the nonlinear system using the full approximation scheme of the space-time multigrid method. The proposed space-time multigrid is a natural fit for solving the data assimilation optimal control system, because the optimization constrained by the nonlinear dynamical model can be solved on a sequence of low-resolution space-time operators with computational efficiency. This process can be simply depicted by J m,J c,J cst, which denote cost functions at various resolutions, in Fig. 1. The technical novelty of the parallel-in-space-time optimization algorithm will be presented and discussed in detail at the symposium.
講師プロフィール
- 名前
- Xinfeng Gao∗
Milija Zupanski+
Jacob B. Schroder†
Robert D. Falgout‡ - 所属
- ∗Colorado State University, CFD and Propulsion Laboratory, Fort Collins, Colorado, USA
+Cooperative Institute for Research in the Atmosphere, Fort Collins, Colorado, USA
†University of New Mexico, Department of Mathematics and Statistics, Albuquerque, New Mexico, USA
‡Lawrence Livermore National Laboratory, Center for Applied Scientific Computing, Livermore, California, USA
他の講義を探す
(2021年1月8日)
