研究内容

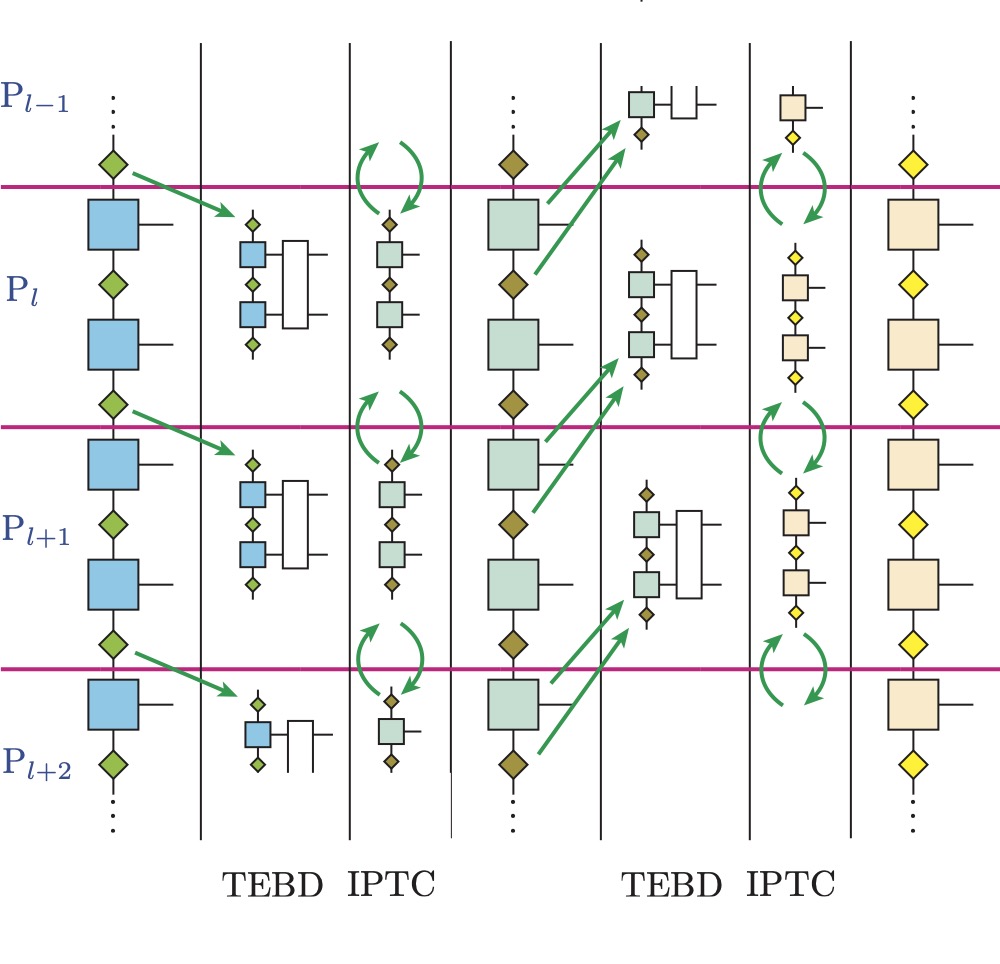
次世代の計算技術の一つとして、量子コンピューティングは近年大きな注目を集めています。現在の量子コンピュータは数百量子ビット程度であり、ノイズに影響されやすいため、Noisy intermediate-scale quantum（NISQ）デバイスと呼ばれています。現在は、そのようなNISQデバイスを効果的に活用できる問題を特定することに多くの関心が寄せられています。このためには、ノイズの影響がない状態で方法論自体の性能を検証し、同時にノイズの影響を調べることが重要です。この目的のために、量子コンピュータの動作をエミュレートする量子計算シミュレータが幅広く利用されています。量子コンピュータのシミュレーションは、量子情報を扱うために指数関数的に大きな計算リソースとメモリを必要とするため、困難な問題です。そこで、私たちは、効率的に量子情報を圧縮する技術として、テンソルネットワーク法に基づく計算アルゴリズムを開発しています。特に、私たちは富岳のような高性能計算（HPC）システムを使用したテンソルネットワーク法の並列化技術に注目しています。

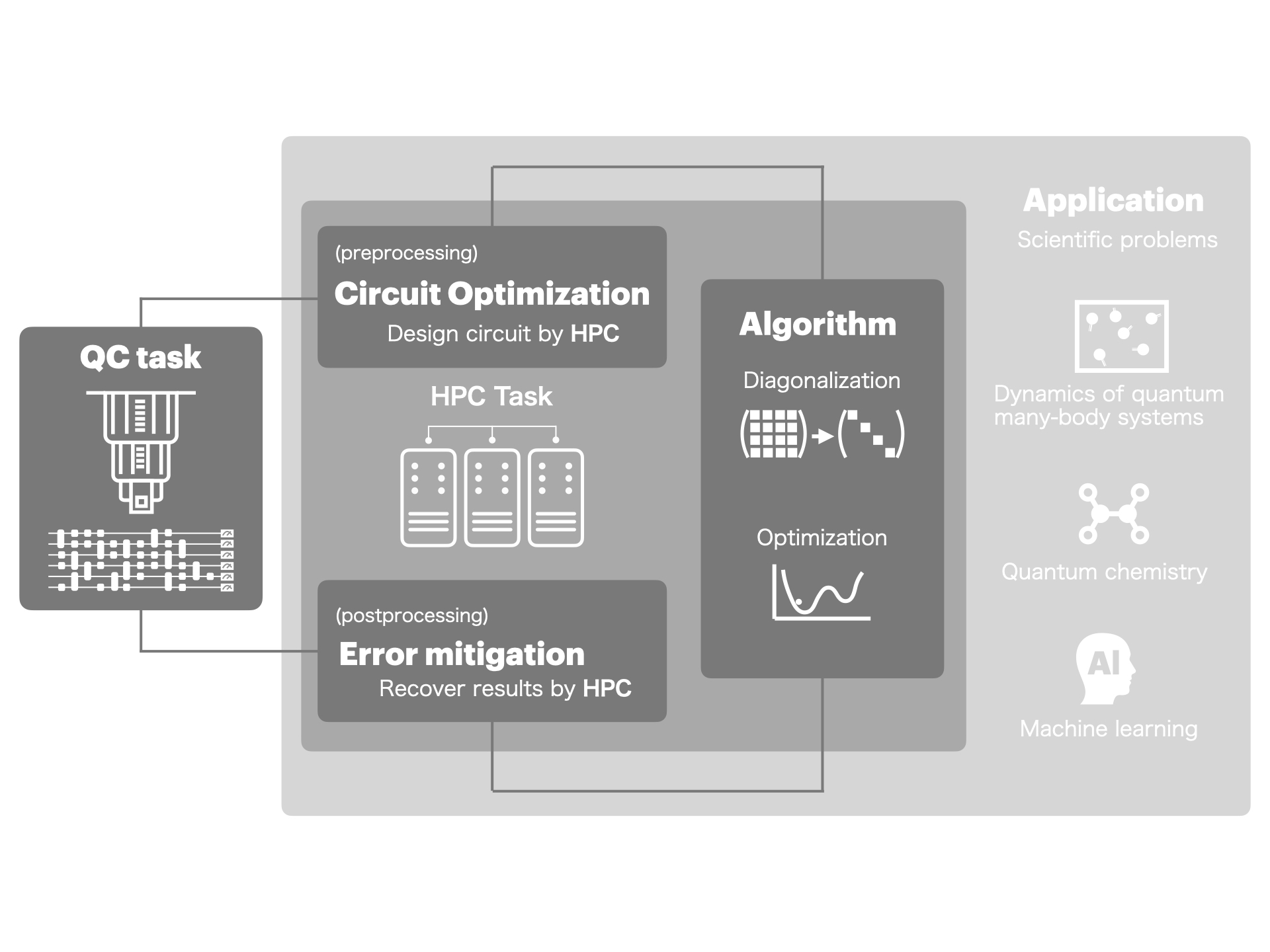
現在利用可能な量子コンピュータは、100程度の量子ビットを持つノイズの大きなデバイスです。一方で、厳密な計算が可能な量子ビット数は、富岳クラスのスーパーコンピュータのメモリを全て用いた場合でも50量子ビット程度が限界です。すなわち、現状の量子コンピュータは古典計算機で厳密計算可能な領域をすでに超えているものの、依然としてノイズの問題に直面しています。そこで、我々はこのような量子計算機を有効に利用できる問題の探索や、ノイズの影響下でも有用な量子アルゴリズムの開発に取り組んでいます。これに並行して、スケーラブルな量子回路を扱う最適化技術や、ノイズの影響を実質的に軽減するためのスケーラブルなエラー抑制技術など、古典計算機のHPC技術を駆使して、厳密計算可能範囲を超える規模の量子コンピュータの量子情報処理をサポートする技術開発も進めています。

密度行列繰り込み群(Density Matrix Renormalization Group: DMRG)法は、一次元的な構造を持つ量子多体系の数値的計算手法として最も効率的な手法の一つとして知られています。計算の目的とする物理量を適切に表現する基底のみでその計算を実行するDMRG法は、指数関数的に増大する量子多体系の内部自由度を一定の範囲に留めることにより、数値的厳密な手法では非現実的なサイズの系の計算を可能にします。
その一方、このDMRG法の多次元系への適用は、その計算精度を保つために必要とされる基底の数が非常に巨大になるため、その計算コストも非常に巨大になります。しかしながら、近年の計算機科学の発展により、密度行列繰り込み群法の二次元系への適用は十分現実的となっています。また、量子モンテカルロ法ではいわゆる負符号問題のため適用が困難な系に対しても適用が可能であることなど、密度行列繰り込み群法を多次元系への適用には非常に大きな意義があります。
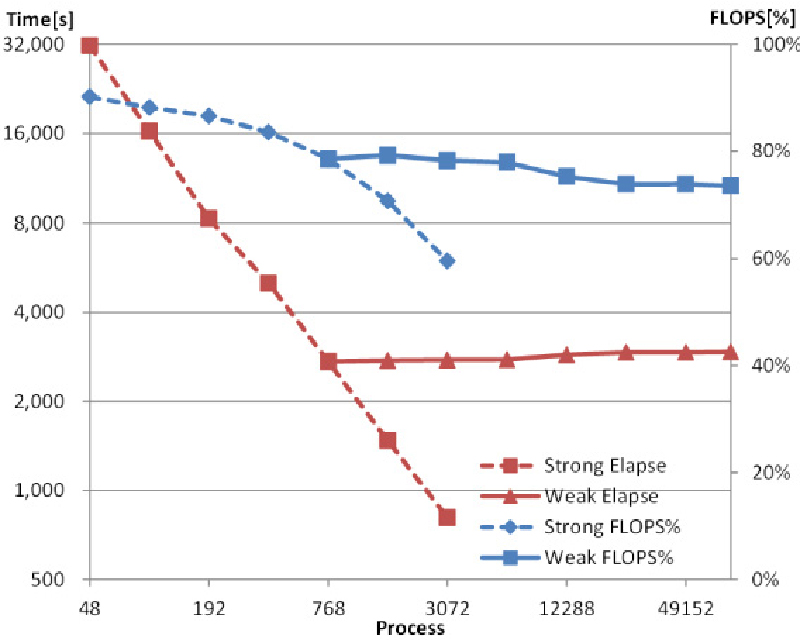
本研究チームでは、このような多次元強相関系への適用を想定した大規模並列密度行列凝りこみ群法の開発に取り組んでいます。開発された密度行列繰り込み群法プログラムは、「京」全ノードを用いた実行で理論性能比70%以上(約7.8 PFLOPS)の実行性能を達成しており、非常に効率的な計算を実行することが可能です。開発された大規模並列DMRG法プログラムは、各種用途に応じて「Dynamical DMRG」、「2-D DMRG」、「paraDMRG」として公開しており、随時講習会も開催しています。

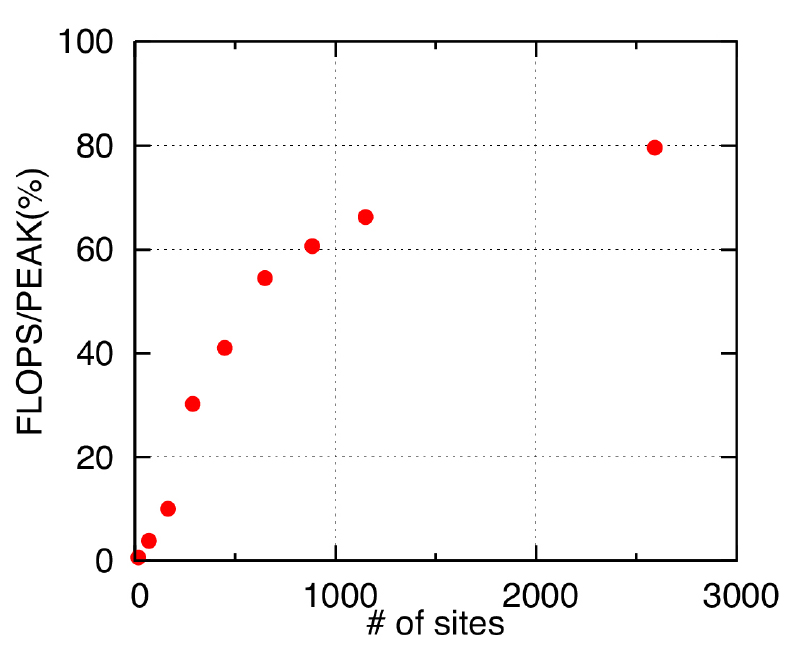
強相関電子系の物性を近似によらず調べるため、補助場量子モンテカルロ法の研究開発を行っている。基底状態に対する補助場法は、ハミルトニアンを肩に持つ指数関数演算子による射影操作で任意の初期状態から基底状態を求めるスキームとなっている。この射影を行う際に補助場自由度を導入することで、計算コストは系のサイズ(N)に対してN3に抑えられるため、非常に大きな系の性質を高精度で調べることが可能となる。我々の実装では初期波動関数の選択を工夫することで、高速に基底状態へ漸近することを可能とした。また、キャッシュを有効利用するためのdelayed update法や、丸め誤差の積算を防ぐための特異値分解に関して計算コストの少ないアルゴリズムを選択することで計算コードの最適化を行った。その結果、「京」1ノード当たりの単体性能については最高で理論性能の80%程度まで達成することを確認した。実際の研究例としては、グラフェンの有効模型であるハニカム格子上のハバード模型に関して計算を行い、この模型に関する先行研究ではN=628までの計算が最大であったのに対し、サイト数で4倍のN=2592（計算規模に関しては約100倍）までの計算を実現した。

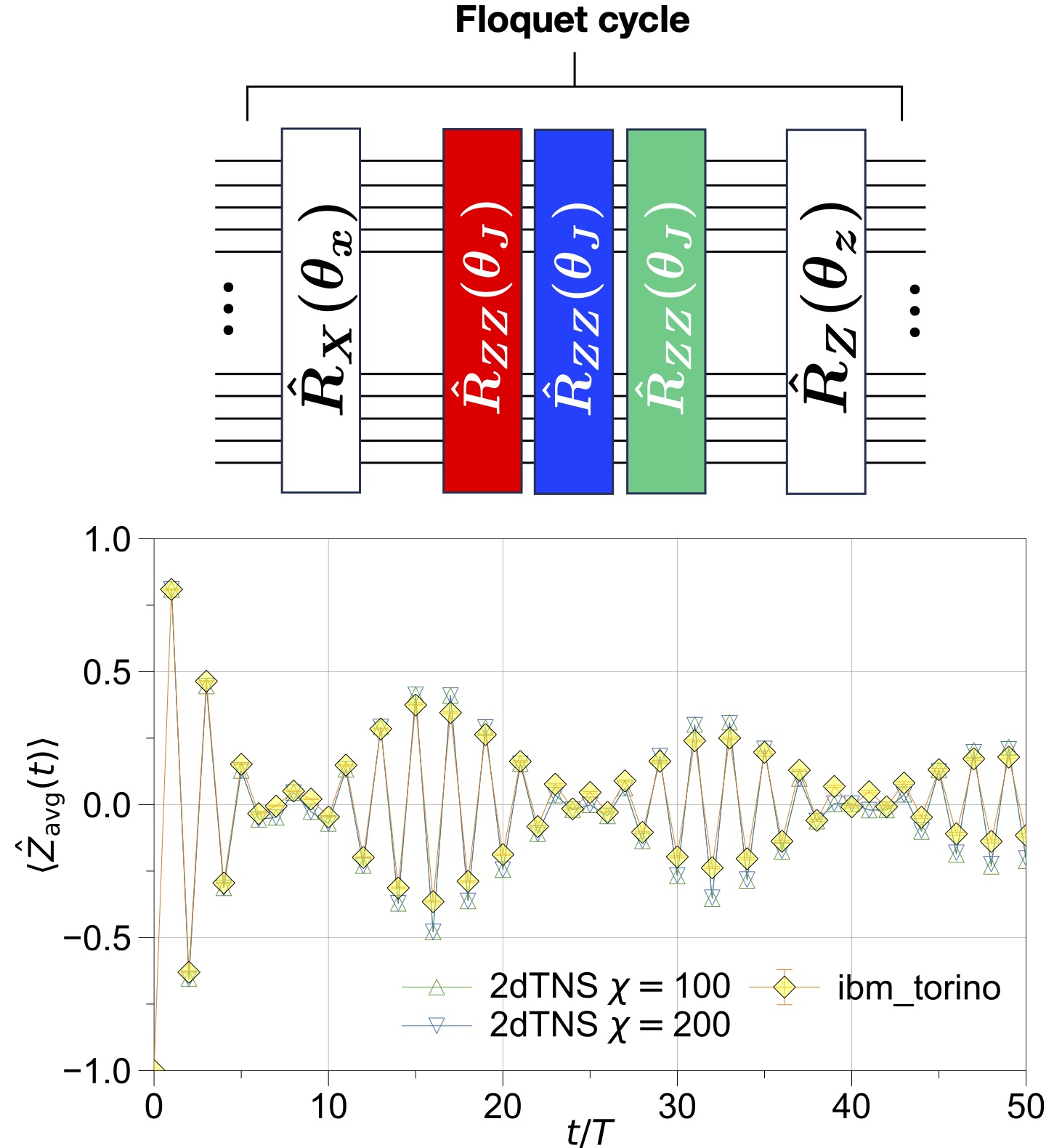
量子多体系の非平衡ダイナミクスは古典計算機でシミュレーションすることが極めて困難であり、100を超えた量子ビットを持つ量子コンピュータの重要なアプリケーションとして近年注目を集めています。 量子コンピュータ実機では、初期化された量子ビット配列に対して量子ゲートを再帰的に演算することにより、いわゆるトロッター化されたユニタリ時間発展を容易に実現することができます。 このような回路はフロッケ量子回路と呼ばれており、ハミルトニアンで記述される連続的な時間発展とは異なる多様な非平衡量子現象の研究舞台を与えています。 私たちは、現在利用可能な量子コンピュータとHPC技術を駆使した古典計算手法とを組み合わせることにより、フロッケ量子回路における新奇なデジタル量子ダイナミクスを探索しています。 最近の研究では、二次元周期駆動系における離散的時間結晶状態などの古典計算機では記述が難しい量子ダイナミクスへの応用を目指し、エラー軽減法の一般化に取り組んでいます。

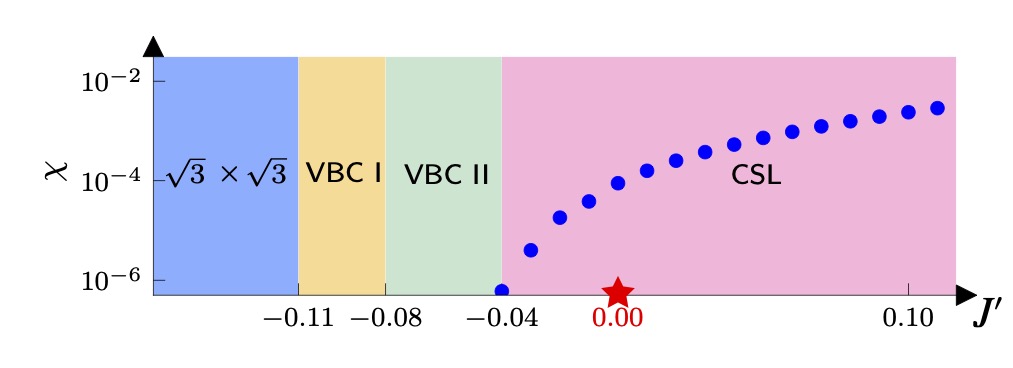
S=1/2 カゴメハイゼンベルグ反強磁性体の基底状態の性質は、量子磁性における至高の探究問題の一つであり、何十年にもわたって議論されてきました。そこで、私たちは、大規模な密度行列繰り込み群計算を実施し、この困難な問題を再検討しました。その結果、その基底状態がカイラルスピン液体（Chiral Spin Liquid, CSL）であることを明確に証明しました。この状態は、時間反転対称性を破り、μ＝1/2のKalmeyer-Laughlin型トポロジカル秩序によって記述される状態です。私たちは、この基底状態が、以前に観測されたより堅牢なカイラルスピン液体相に断熱的に接続可能であることを実証しました。さらに、この相の付近を調査してみると、√3×√3磁気秩序相と、２種類のvalence-bond crystal相（VBC IとVBC II）が存在することを発見しました。

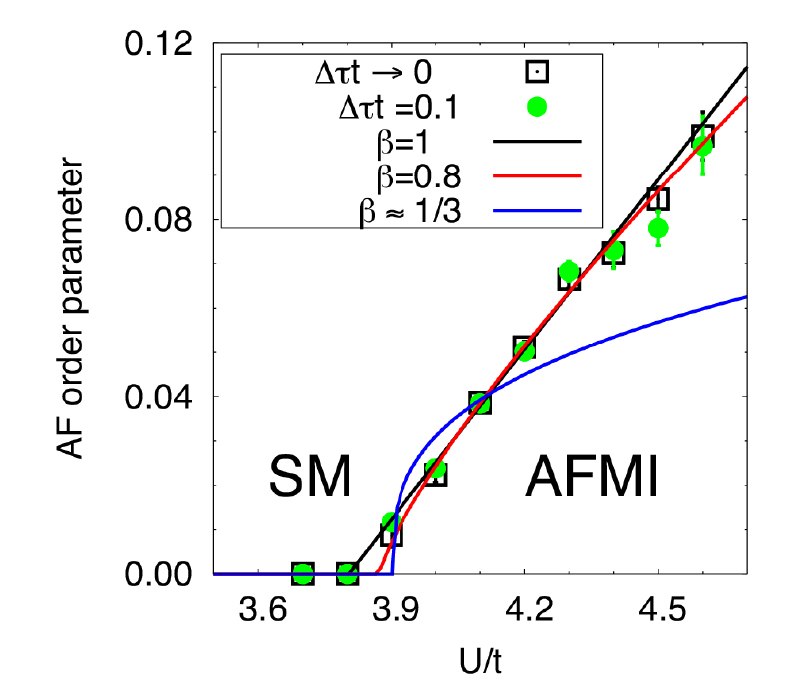
相互作用を持つにも関わらず絶対零度まで秩序化を起こさない「スピン液体相」の探索は現在の物性分野において最も精力的に研究されているトピックの一つとなっている。
通常、スピン液体相の実現のためには強い量子効果のみならず、幾何学的フラストレーションのような競合効果が必要と考えられていた。 しかし、2010年にそのようなフラストレーションが生じないハニカム格子上のハバード模型においてスピン液体相が存在するとの報告がなされ、大きな注目を集めた。
この模型では弱相関領域ではディラック電子系による半金属相、強相関側では（フラストレーションがないため特に）反強磁性絶縁相が安定となるが、先行研究ではこれら二つの相の間にある程度の相領域を持つスピン液体相が量子効果のみで生じるとの主張がされた。 我々はこの問題に対して、より大規模な格子模型を対象とした高精度なシミュレーションを行うことで再検討を行い、スピン液体相はたとえ存在するにしても非常に弱く、むしろ反金属相から反強磁性絶縁相への直接連続転移であることを強く示唆する結論を得た。

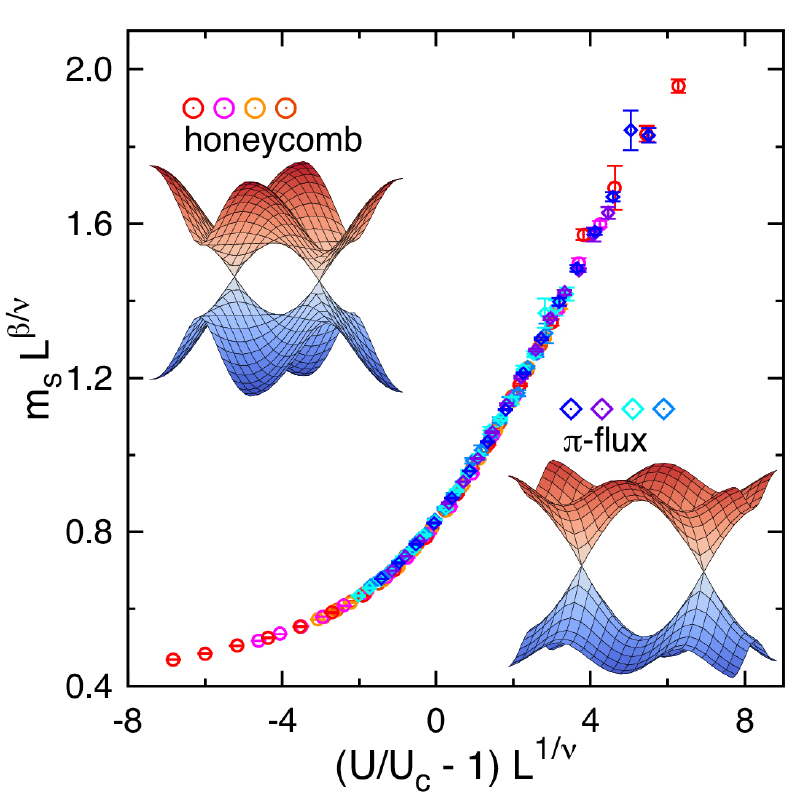
ハニカム格子等で見られる分散関係がフェルミ面近傍で線形となるディラック電子系では、ネスティング不安定性や状態密度の発散を伴う正方格子系とは異なり、有限の強さの相互作用まで反金属相が安定となり、モット転移の性質を調べる格好の舞台となっている。 我々はハニカム格子およびπフラックス模型と呼ばれる、ディラック電子系が構成される二つの異なる格子模型を対象として、ハバード型斥力による常磁性半金属相から反強磁性絶縁相への量子相転移の臨界的な性質を大規模量子モンテカルロシミュレーションにより調べた。その結果、これら二つの格子模型における転移の臨界指数は高い精度で一致し、ディラック電子系におけるモット転移には普遍性クラスが存在することを数値的に実証した。 これらの系は連続極限において、古くから素粒子物理で議論されていたGross-Neveu模型と同等となることが知られおり、我々が得た臨界指数はこの模型におけるchiral-SU(2)対称性の破れを記述するものでもある。