ヒト脳理解に向けてのスタートライン

私たちが運動したり、考えたり、話したりするとき、脳の中では神経細胞が相互に信号をやりとりしながら活動しています。その数はなんと860億個! 五十嵐さんたちは、ポスト「京」を用いて、このうちの99%の活動をシミュレーションしようという壮大なプロジェクトを進めています。
シミュレーションは脳研究の切り札
「高校生のころ、ニューラルネットワークという、脳が行っている情報処理をコンピュータ上で再現する研究がさかんになり、そのときに読んだ本で『脳をまねる』ということに興味をもちました」という五十嵐さん。大学院時代から脳のシミュレーションに取り組んできました。「京」を用いて、「できるだけ多くの神経細胞の活動をシミュレーションする」課題と、「脳の信号が脳内のさまざまな部位を通って体を動かすまでを再現する」課題に参加して、大きな成果をあげ、2016年からは、ポスト「京」の萌芽的課題「思考を実現する神経回路機構の解明と人工知能への応用」のメンバーとして、全脳規模シミュレーションに向けた研究を進めています。
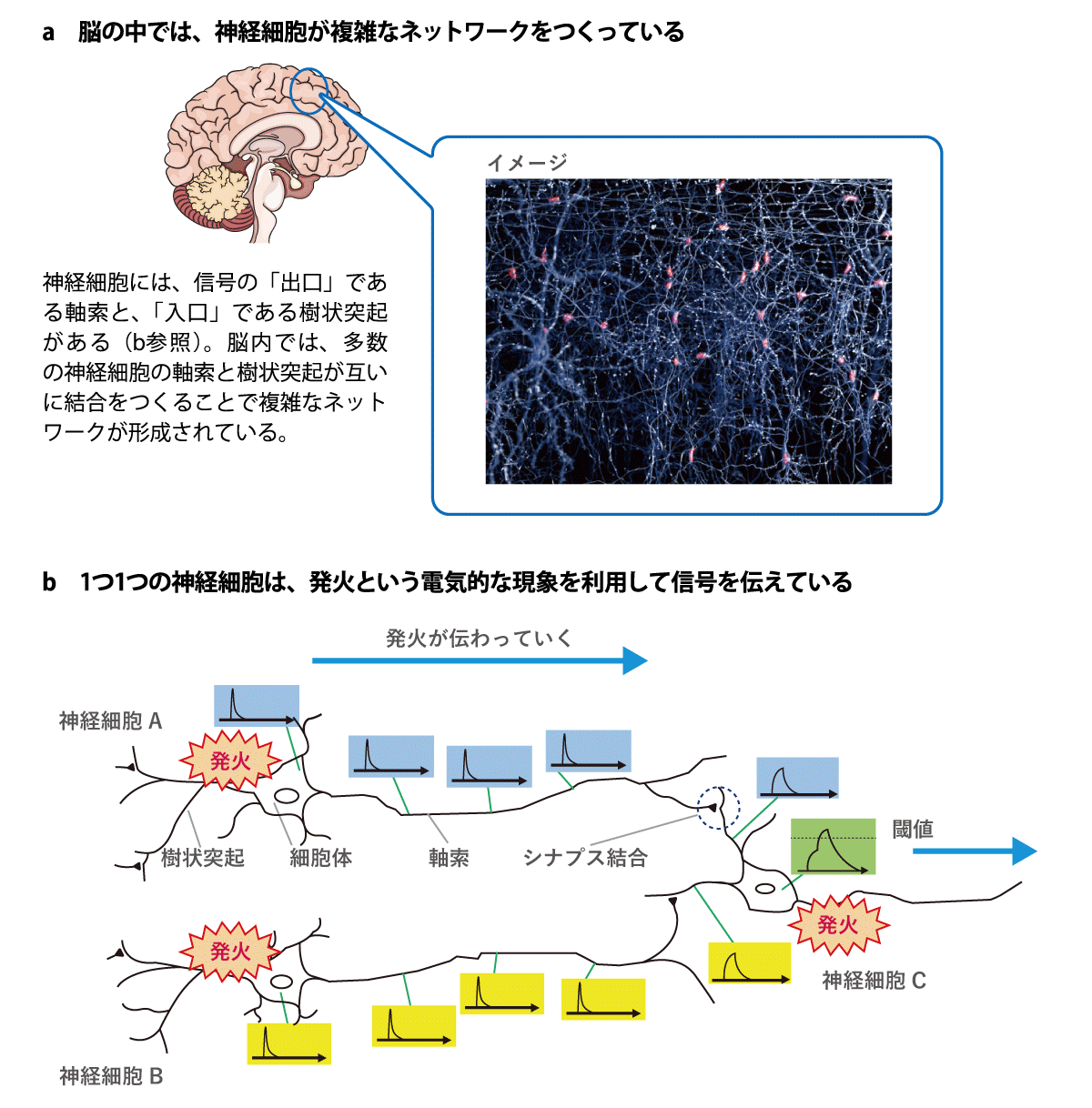
私たちの脳は、高度な認識・学習能力をもち、多様な問題に柔軟に応答し、創造性を発揮します。しかも、消費エネルギーはわずか約10Wと「超省エネ」です。しかし、このような能力がどのようなしくみで発揮されるのかは、未解明です。「その理由は、脳の構造が非常に複雑だからです」と、五十嵐さんはいいます。脳には情報を処理する神経細胞が約860億個もあります。その上、1個の神経細胞からの信号の「出口」である軸索の先はたくさんの枝に分かれており、他の細胞からの信号の「入口」である樹状突起もたくさんあります(図1a)。これらが相互に結合をつくっているため、結合の数は全部で100兆個以上もあると見積もられています。

「すべての神経細胞の活動や、結合を介しての信号のやりとりを、実験で把握することはまだ非常に難しい状況です。一方、シミュレーションではすべて記録することができ、脳の一部だけとか、ある病気になったときの脳というように、どんな状態でも、何度でも調べることができます。シミュレーションは、脳のしくみを研究するための非常に有力な方法なのです」
神経細胞を電気回路だと見なす
脳のシミュレーションはどのように行うのでしょうか。それを知るには、まず、神経細胞の活動について知っておく必要があります(図1b)。
脳の複雑なネットワークの中で、神経細胞は「発火」することによって、信号を互いに伝えあっています。発火とは、一時的に細胞内の電位が高くなる現象のことです。刺激を受けた神経細胞の細胞体で発火が起こると、その発火は波のように軸索を伝わっていき、シナプス結合を介して次の神経細胞に信号が伝わります。1つの神経細胞には多数の神経細胞から信号がやってきますが、その合計がある値(閾値:しきいち)を超えたときにだけ発火し、次の神経細胞に向けて信号を送り出します。
「このような神経細胞の活動は、電気回路のモデルに置き換えることができます。脳のシミュレーションでは、たくさんの神経細胞モデルをスパコンのなかで結合し、発火による信号の伝達を行わせ、時間が経つにつれて個々の細胞の活動がどう変化していくかを計算します」
しかし、話はそれほど単純ではありません。まず、発火の仕方は神経細胞の種類によって異なります。また、神経細胞どうしの結合の強さ(信号を伝える強さ)は神経細胞のペアごとに異なり、しかも、発火が何度もやってくると変化します(実は、これが私たちの「学習」のおおもとのしくみなのです)。さらに、神経細胞の配置は脳の部位ごとに異なり、その配置が結合の数や強さに影響します。1つの神経細胞の活動の特性を決める値(パラメータ)は山ほどあるのです。
幸いなことに、2000年以降、脳の各部位の神経細胞の種類や、脳内の神経細胞どうしの結合を調べる技術が急速に発達し、このようなパラメータについて膨大なデータが加速度的に蓄積されています。その一方で、スパコンの性能も向上し、次第に大規模な脳のシミュレーションが行われるようになってきています。こうした中で、2013年、「京」の全体を用いて、17.3億個の神経細胞が10.4兆個の結合でつながっている場合の、当時としては世界最大規模のシミュレーションが成功しました。
五十嵐さんは、この研究のメンバーの一人でした。「この研究は、『京』でどれだけの神経細胞の計算が可能かという技術的限界を調べることが主目的でした。17.3億個の計算ができたので、『京』の100倍の計算性能をもつスパコンができれば、全脳のシミュレーションが可能だという見通しが立ちました」
パーキンソン病の腕の震えを再現
次に、五十嵐さんは、パーキンソン病のシミュレーションに取り組みました。この研究は、「京」を用いたHPCI戦略プログラムの課題の1つとして2011-16年に行われました。
パーキンソン病では、動作の困難、手足の震え、筋肉の硬直などの症状が現れます。脳内のドーパミンが枯渇することが原因ですが、このような症状が現れるしくみはよくわかっていません。
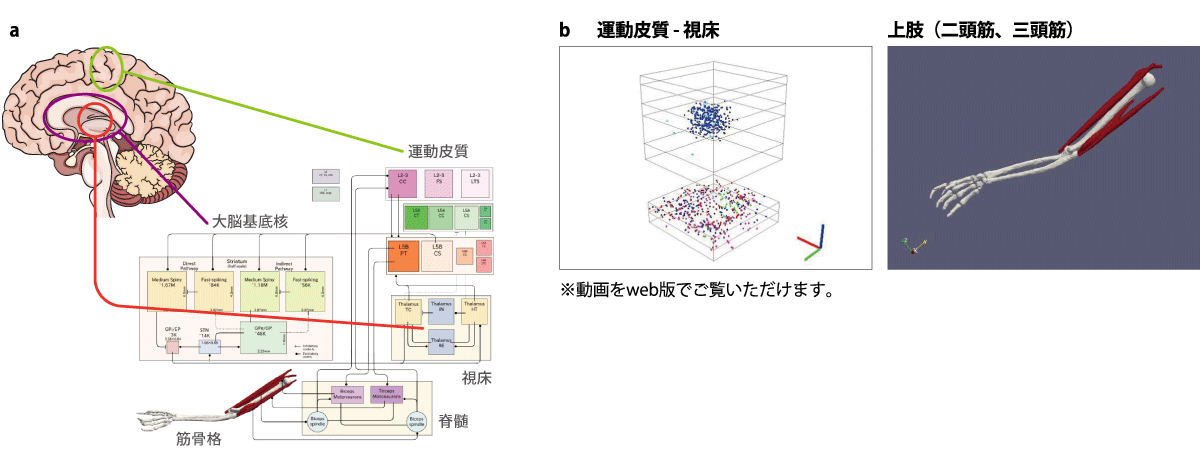
私たちが体を動かすとき、運動の命令は、大脳皮質の運動野(運動皮質)から脊髄を通して筋肉に伝わります(図2上)。そして、ドーパミンは、この命令の流れの途中にある大脳基底核に働きかけることがわかっています。そこで、五十嵐さんが当時所属していた沖縄科学技術大学院大学(OIST)、東京大学、大阪大学のグループは共同で大脳基底核-視床-運動皮質-脊髄-筋骨格の統合モデルをつくり、腕の震えの再現に取り組みました。このモデルは、部位による神経細胞の性質の違いを採り入れるなど、現実に近いもので、約300万個の神経細胞を用いて6秒分のシミュレーションを行いました。
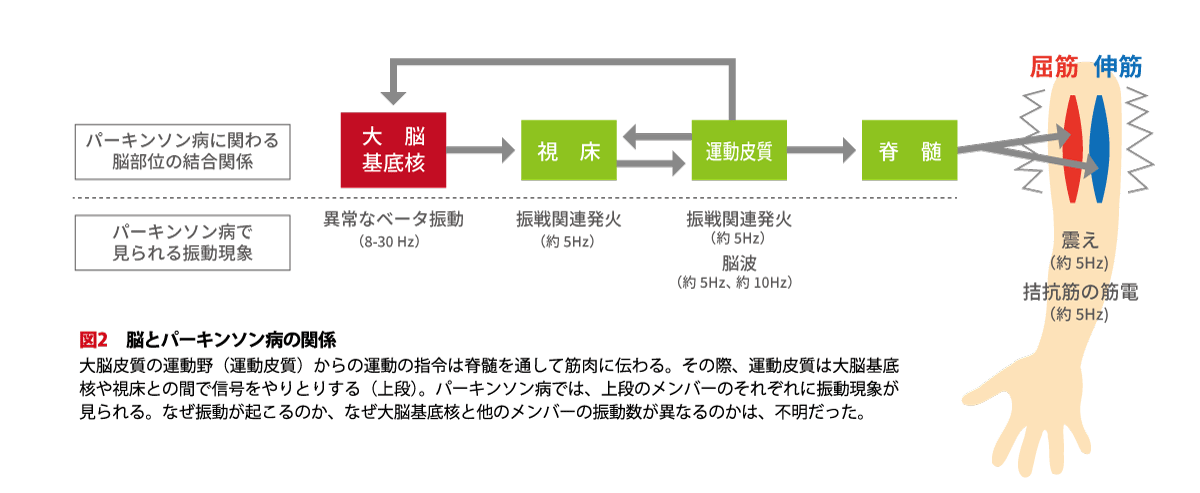

「患者さんでは大脳基底核でベータ波(脳波の一種)の異常な振動(8-30Hz)が見られ、手足が約5Hzで震えることが知られています(図2下)。ドーパミン枯渇を想定したシミュレーション(図3)では、大脳基底核で約15Hzの異常なベータ振動が見られ、運動皮質から6-7Hzで腕の震えを起こすような信号が出ていましたが、健常者を想定した場合にはどちらも現れませんでした。つまり、このシミュレーションは、ドーパミン枯渇で大脳基底核に振動が生じ、さらに、それとは異なる振動数で腕が震えるしくみを知る手がかりを与えてくれたのです」
b aのモデルで、ドーパミン枯渇状態を想定したシミュレーションを行ったところ、運動皮質と視床では6-7Hzの振動が起こり、腕の震えのような動きを引き起こした。健常人を想定した場合は、振動は起こらなかった。

大きな目標に向けて課題を1つずつ解決
そして今、五十嵐さんたちは、全脳規模のシミュレーションに向けて準備を進めています。脳の全神経細胞のうち99%は大脳と小脳に含まれているため、大脳と小脳を対象とする計画です。五十嵐さんは大脳皮質を担当し、OISTの銅谷賢治教授が大脳基底核、電気通信大学の山﨑匡准教授が小脳を担当します。
「京」での17億個を、ポスト「京」での860億個にするためには、神経回路シミュレータというソフトウェアの性能が重要です。脳のシミュレーションでは1つの計算ノード(スパコンは小さなコンピュータの集まりであり、その1つ1つを「計算ノード」と呼ぶ)に多数の神経細胞の計算を担当させる必要がありますが、神経回路シミュレータはその割り振りを自動的に行ってくれます。
「京」での計算に用いたNESTシミュレータは、細胞の数が増えると通信量がどんどん増えてしまい、その分計算が遅くなるという問題がありました。そこで、NESTの開発元のドイツのグループがデータの構造と通信方式を改良し、日本側では「京」での試験を行った結果、通信量を抑えることに成功しました。
もう1つ重要なのは、脳の神経回路の構造を採り入れることです。「大脳皮質と小脳は神経細胞が並んだシートが層状に重なったものです。そのため、1つの神経細胞は近くの細胞とは密な結合をもっていますが、遠くの細胞との結合は少ないのです」。これをポスト「京」で効率的に計算するため、五十嵐さんは新しい神経回路シミュレータを開発しました。このシミュレータでは、大脳皮質を面積が1平方ミリメートルのタイルに区切り、1個のタイルを1個の計算ノードで計算します(図4a)。
すでに、「京」を用いて大脳皮質の10分の1にあたる16384平方ミリメートルの面積に含まれる数億個の神経細胞の活動を3秒間にわたって計算することに成功しています(図4b)。さらに、大脳皮質、視床、小脳からなる脳のモデル(約10億個の神経細胞)のシミュレーションにも成功し、活動の可視化(約1000万個の神経細胞)も達成しています。
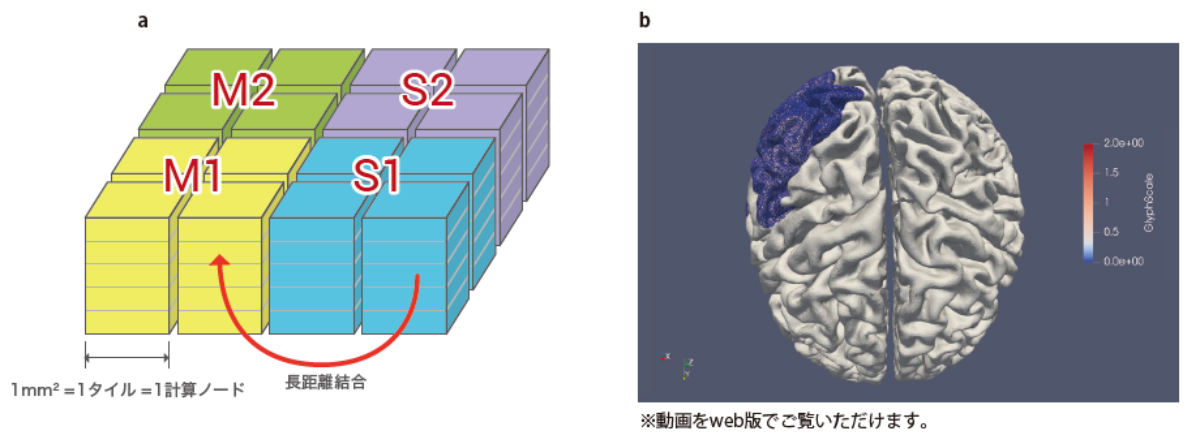
b aの方式で、大脳皮質のうち16384平方ミリメートルの神経細胞の活動を「京」でシミュレーションすることができた。計算は6層について行ったが、ここでは可視化の制約から第1層のみ(図の青の点群)を示す。

着々と準備が進む全脳規模シミュレーション。実現すれば、脳のしくみがわかるのでしょうか。「このシミュレーションでわかることはたくさんあると思いますが、脳の高次機能を理解するには、大脳と小脳以外の部位も含めるなど、さらに現実に近いものにブラッシュアップしていくことが必要です。全脳規模のシミュレーションが成功しても、それはスタートラインに過ぎないのです。ただし、そのスタートラインにはまだ誰も立ったことがないので、大きな変化が起こると期待しています」と五十嵐さんは答えてくれました。
脳のしくみが解明されれば、脳の病気の治療、学習の効率化、人工知能への応用といった効果が期待されるだけでなく、「人間とはなにか」という哲学的な問いへの答えが得られるかもしれません。そうした将来に向けて、五十嵐さんをはじめ、多くの研究者がこれからも挑戦を続けていくことでしょう。
(取材・執筆:サイテック・コミュニケーションズ 青山聖子)
に収録されています。