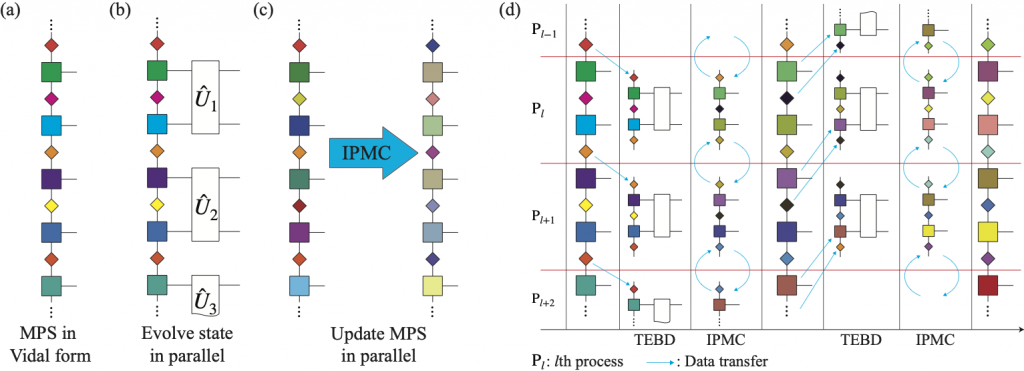
Based on the matrix-product state (MPS), a typical tensor network state [see Fig. (a) above], we proposed a real-space fully parallelizable simulation algorithm (improved pTEBD) to efficiently simulate unitary quantum dynamics, which is the key to understanding non-equilibrium quantum phenomena and quantum computations. In this algorithm, each layer of a quantum circuit (a generic representation of unitary quantum dynamics) can be simulated in parallel [see Fig. (b) above] and the resulting MPS is further compressed by the improved parallel MPS compression (IPMC) method [see Fig. (c) above]. IPMC enables efficient compression of all virtual bonds in constant time, irrespective of the system size, with controlled accuracy, while it maintains the stability of the wave-function norm without necessitating sequential renormalization procedures. The complexity of this algorithm is O(1) in contrast to the at least O(N) (N is the system size) complexity in typical tensor network algorithms. The schematic plot of the improved pTEBD algorithm is in Fig. (d) above.

We employ the improved pTEBD algorithm for extensive simulations of typical one- and two-dimensional quantum circuits, involving over 1000 qubits, on the Supercomputer Fugaku installed in R-CCS. The obtained numerical results unequivocally demonstrate that the improved pTEBD algorithm achieves the same level of simulation precision as the current state-of-the-art MPS algorithm but in a polynomially shorter time, exhibiting nearly perfect weak scaling performance on a modern supercomputer. The details of this study have been published in the following paper.

Journal reference: Rong-Yang Sun, Tomonori Shirakawa, and Seiji Yunoki, “Improved real-space parallelizable matrix-product state compression and its application to unitary quantum dynamics simulation” Phys. Rev. B 110, 085149.
DOI: https://doi.org/10.1103/PhysRevB.110.085149