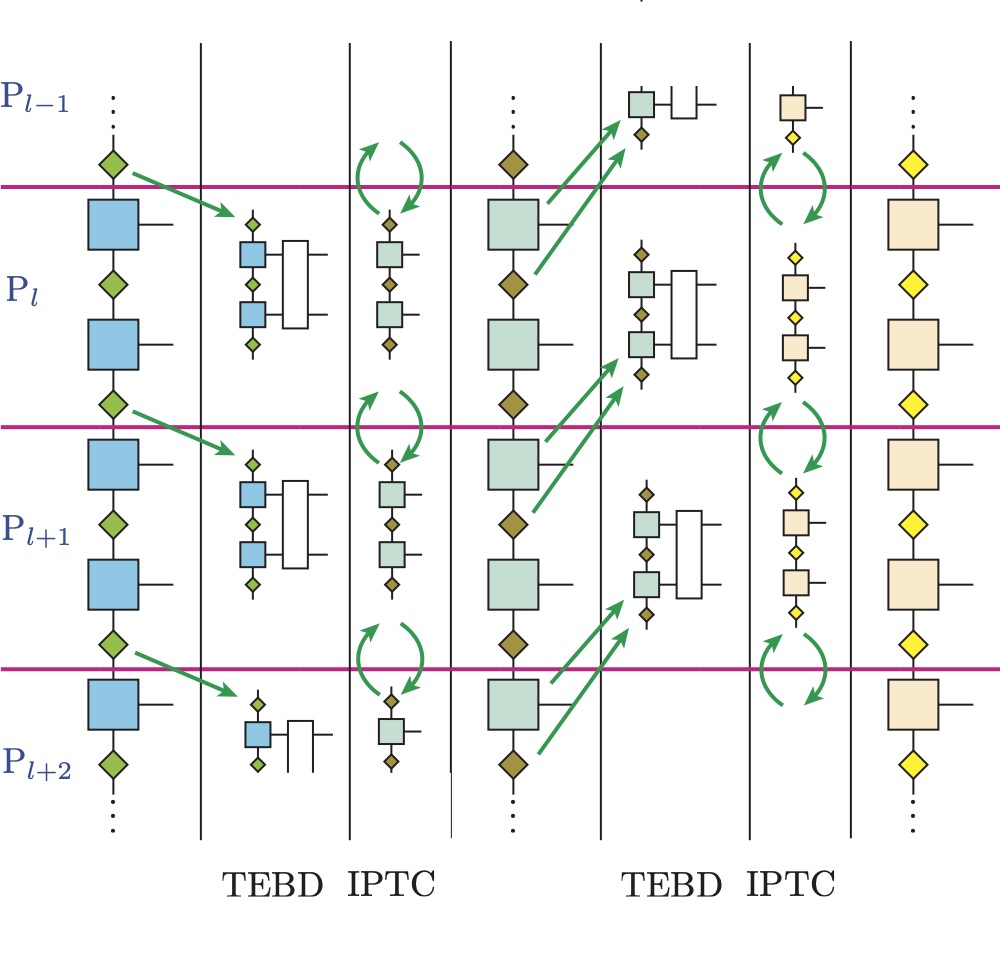
As one of the next-generation computing technologies, quantum computing has garnered significant attention in recent years. Current quantum computers typically have only a few hundred qubits and are susceptible to noise, hence the term noisy intermediate-scale quantum (NISQ) devices. Consequently, much attention has been focused on identifying problems that can be effectively addressed using such NISQ devices. To this end, it is important to validate the methodology itself without noise effects and, simultaneously, examine how it is impacted by noise. For this purpose, quantum computing simulators that emulate the behavior of quantum computers are being widely used. Simulating a quantum computer is challenging because it requires exponentially large computational resources and memory to handle quantum information. Therefore, to efficiently compress quantum information, we are developing a computational algorithm based on the tensor network method. Specifically, we are focusing on parallelization techniques for tensor network methods using high-performance computing (HPC) systems like Fugaku.

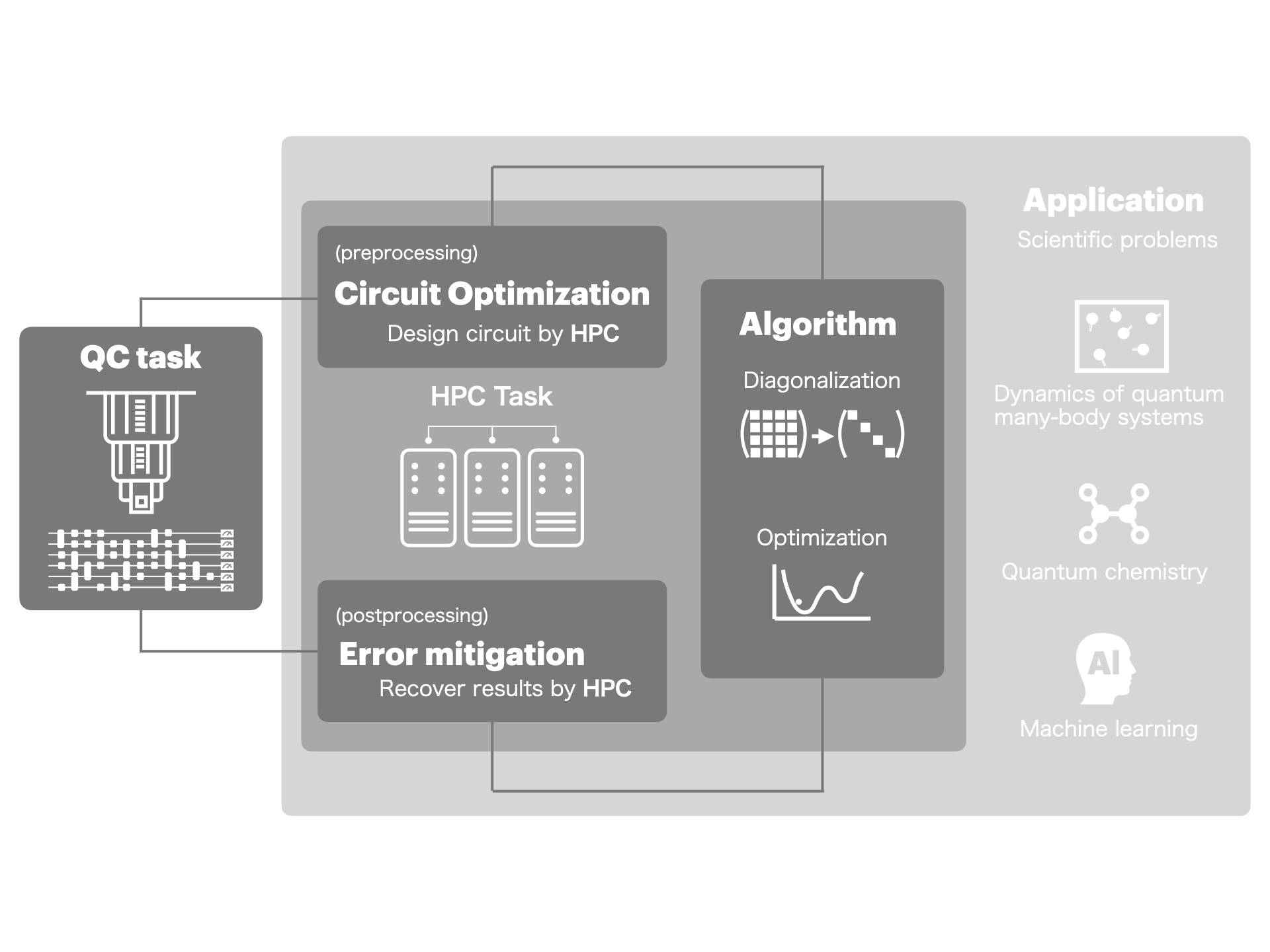
Currently available quantum computers are noisy devices with around 100 qubits. On the other hand, the maximum number of qubits for which exact calculations are possible is limited to about 50 qubits, even when utilizing the entire memory of a supercomputer like Fugaku. This means that while current quantum computers have already surpassed the exact calculation capabilities of classical computers, they still face significant noise issues. In response, we are exploring problems that can be effectively solved by such quantum computers and developing quantum algorithms that remain useful even under noisy conditions. In parallel, we are advancing the development of technologies that support quantum information processing on a scale beyond the exact calculation capabilities. These include scalable optimization techniques for handling large quantum circuits and scalable error suppression techniques to practically mitigate the effects of noise, leveraging HPC technologies from classical computing.

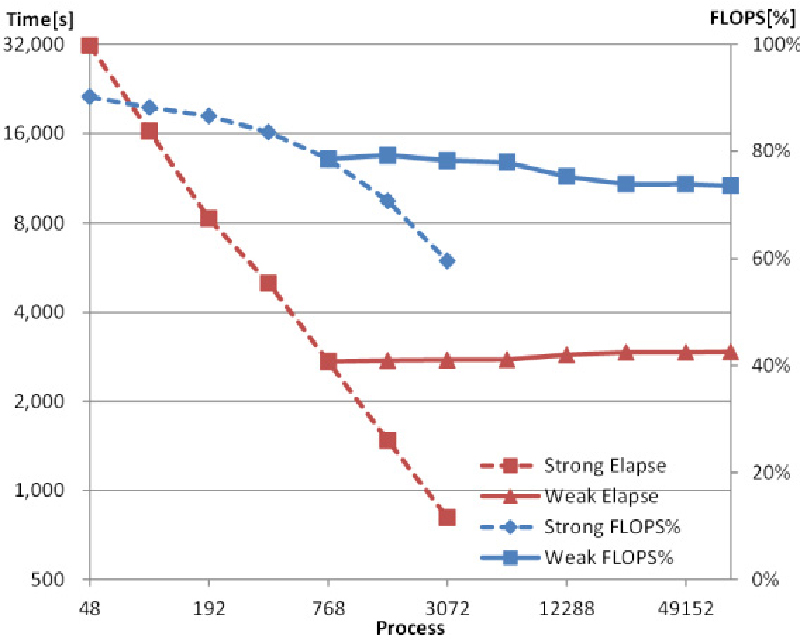
The density matrix renormalization group (DMRG) method is known as one of the most efficient numerical methods for one-dimensional quantum many-body systems. Although the degree of freedom of quantum many-body systems increases exponentially with the system size, the DMRG method can accurately describe the quantum states by an arbitrary number of bases and can treat larger systems that exact numerical methods cannot afford. On the other hand, the DMRG method for higher-dimensional systems requires quite large computational costs to keep its numerical accuracy because of the rapid increase of quantum entanglement. Nonetheless, recently developed large-scale supercomputers enable us to perform accurate DMRG calculations of two-dimensional systems that other numerical methods such as quantum Monte Carlo methods cannot treat because of the notorious negative sign problem. Thus, it is important to develop an efficient massively parallel DMRG algorithm. We have developed massively parallel DMRG codes that have achieved more than 70% (7.8 PFLOPS) for the theoretical performance of the K computer using all nodes (82,944 nodes). Our large-scale parallel DMRG codes are open to the public: "Dynamical DMRG" for quantum dynamics, "2-D DMRG" for higher dimensional systems, and "paraDMRG" for ab-initio calculations of strongly correlated molecules.

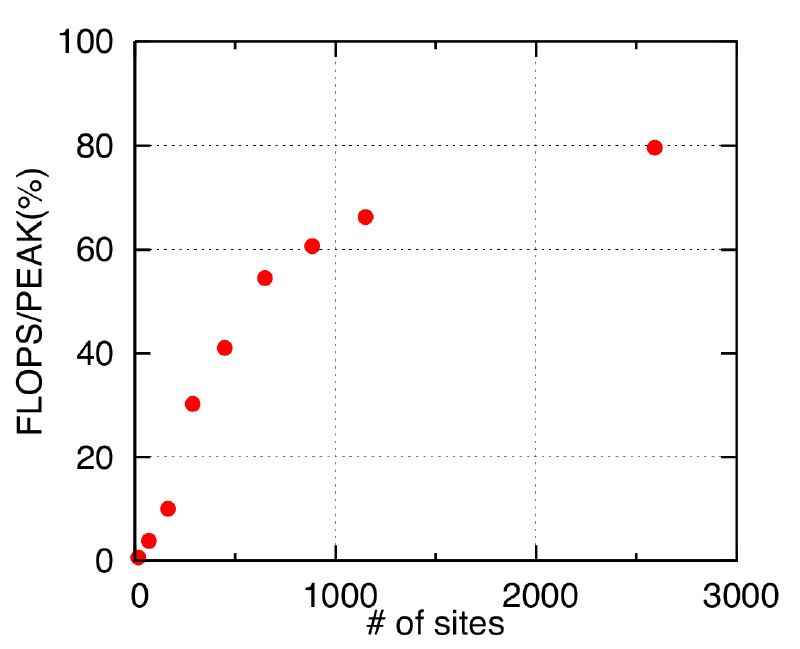
A quantum Monte Carlo (QMC) method is one of the most reliable and efficient techniques for strongly-interacting electrons. We have been engaged in developing a highly efficient QMC code based on the auxiliary field scheme for lattice fermion systems. Since numerical calculations involved in this formulation are mostly linear algebraic procedures such as matrix-matrix product and numerical orthogonalization, we can take full advantage of numerical libraries highly optimized for supercomputers such as K and Fugaku to calculate physical observables with a high degree of accuracy on unprecedentedly large systems. Typical target systems we aim at are of the order of 10,000 electrons and more in two or three dimensions unless the notorious negative-sign problem occurs. Our simulation code has achieved up to 80% of the theoretical performance per node of the K computer, in addition to the inherent suitability of the QMC method for parallel computation. For example, we have successfully performed QMC simulations for the Hubbard model on a honeycomb lattice, a canonical model for graphene, with up to 10,952 sites at half filling to reveal quantum criticality of a metal-insulator transition.

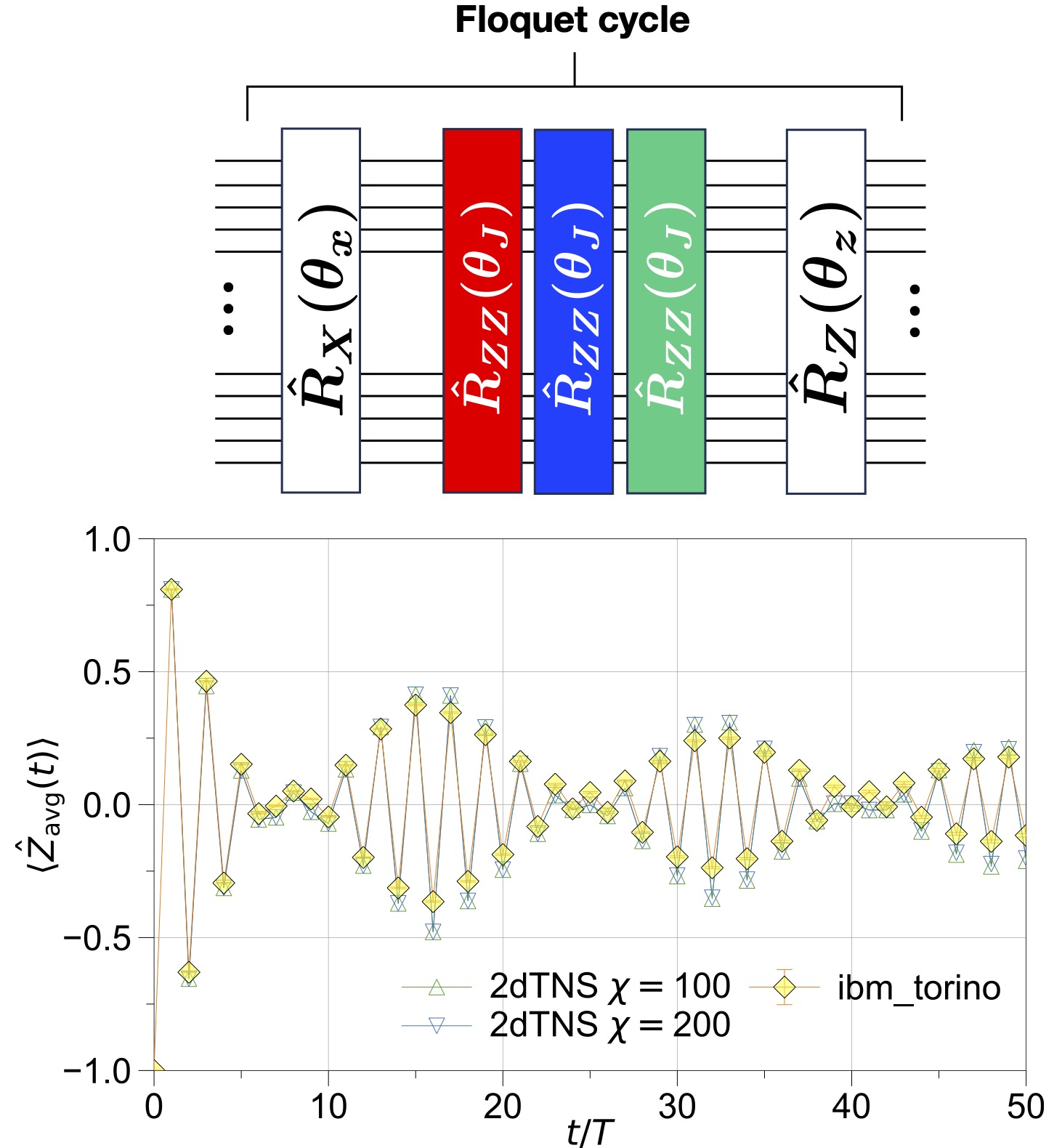
Nonequilibrium dynamics of quantum many-body systems is extremely hard to simulate in classical computers. However, the latest quantum devices involving many qubits more than 100 may crush the inevitable limits in classical computers because these could potentially simulate deep quantum circuits acting on many qubits with the implementation of adequate circuit optimizations and various error mitigation techniques. In the gate-based quantum computers, one can readily realize Trotterized unitary time evolution generated by iterative operations of shallow-depth unitary gates built with primitive quantum gates starting from an initialized configuration of qubits. Such quantum circuits are called the Floquet quantum circuits, offering a new platform of realizing various nonequilibrium quantum phenomena beyond the paradigm of continuous Hamiltonian dynamics. We explore novel digital quantum dynamics in the Floquet quantum circuits by using cloud-based quantum computers and our tailored numerical methods massively parallelized for HPC systems. The recent activities in our team include the attempts to generalize error mitigation techniques for the discrete time crystals in periodically driven two-dimensional systems and others.

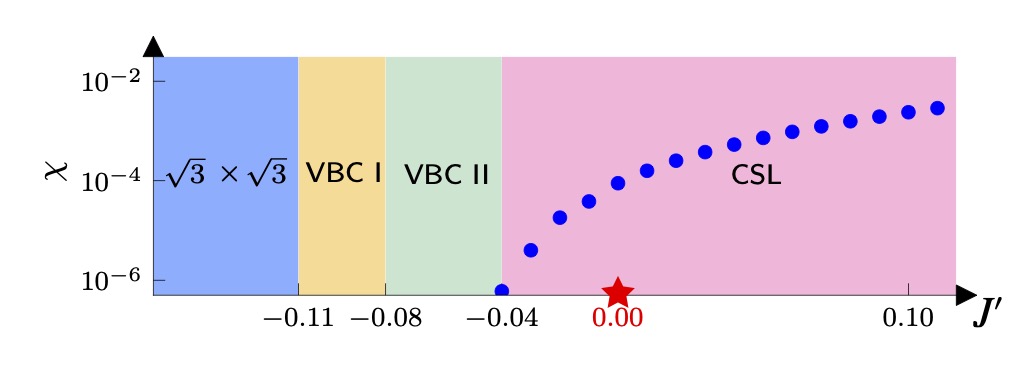
The nature of the ground state for the S=1/2 kagome Heisenberg antiferromagnet (KHAF) is one of the “holy grail” problems in quantum magnetism and has been debated for decades. We revisited this challenging problem with large-scale density-matrix renormalization calculations. These numerical results provided clear evidence that its ground state is a chiral spin liquid (CSL), which breaks the time-reversal symmetry and can be described by a ν = 1/2 Kalmeyer-Laughlin-type topological order. We demonstrated that this ground state is adiabatically connectable to the previously observed robust CSL phase in the KHAF with longer-range couplings. We further investigate the phase diagram in the vicinity of the KHAF and observe a √3×√3 magnetically ordered phase and two valence-bond crystal phases (VBC I and VBC II).

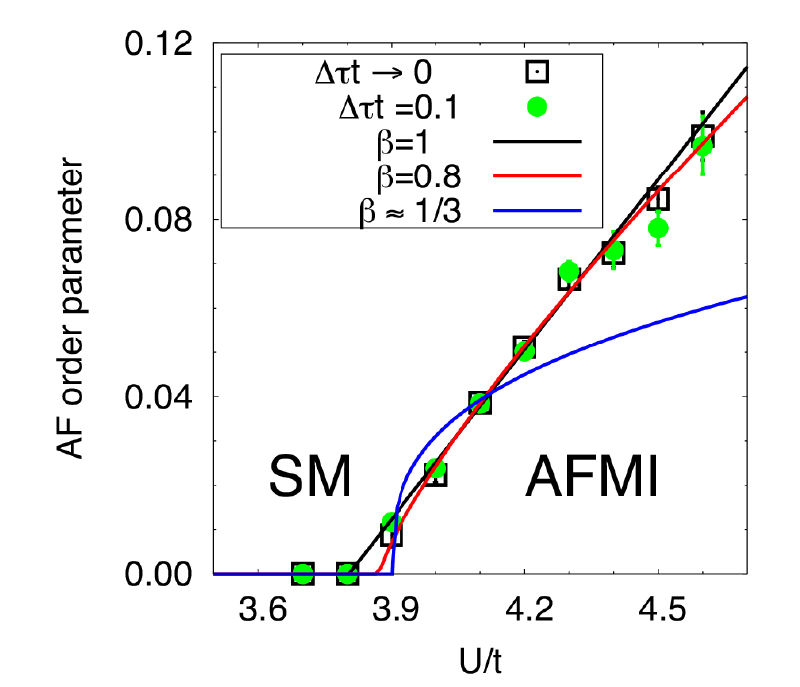
The search for a spin liquid phase, a novel state of matter that exhibits no long-range order despite having mutual interactions, is one of the most challenging subjects in modern condensed-matter physics. Conventionally, it is believed that not only the strong quantum effects but also geometrical frustration is necessary to realize a spin liquid phase. In 2010, a surprising and even controversial proposal was reported; it claims that the spin-liquid phase emerges in the Hubbard model on the non-frustrating honeycomb lattice as an intermediate phase between a semimetal (SM) and an antiferromagnetic Mott insulator (AFMI). We have examined this interesting possibility by performing large-scale QMC simulations and eventually concluded that the spin-liquid phase reported previously is unlikely.

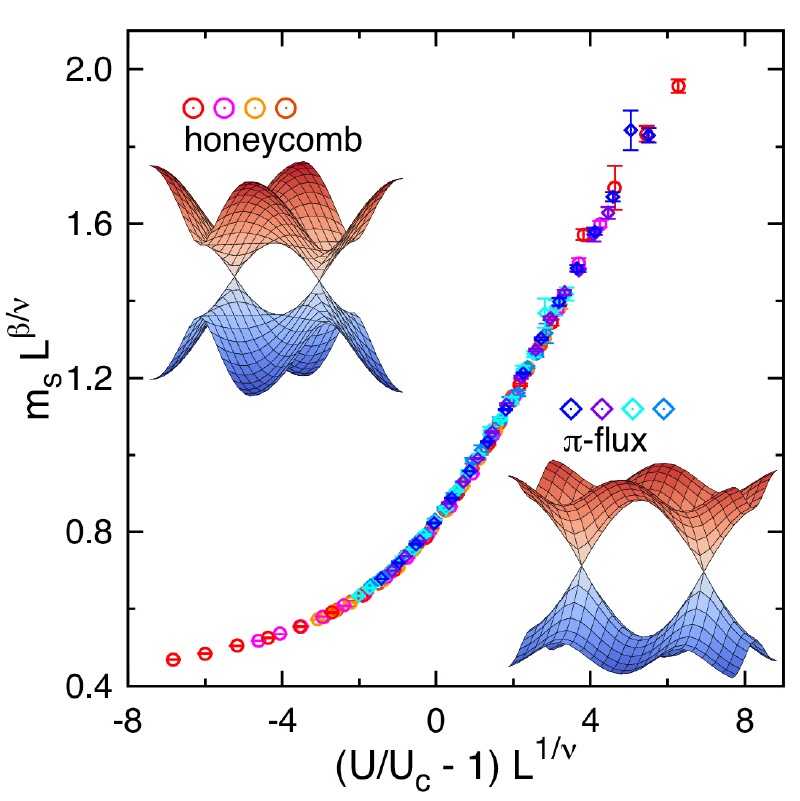
Interacting Dirac electrons constitute an ideal platform to study interaction-driven metal-insulator transitions since it does not involve the nesting instability or the divergence of the density of states, both of which bring about a trivial phase transition even in a weak-coupling limit. We have investigated the quantum criticality of the phase transitions between a semimetal and an antiferromagnetic insulator in the Hubbard model on the honeycomb lattice and on the square lattice with π-flux. By performing large-scale QMC simulations, we have determined critical exponents for the transitions with a high degree of accuracy and found that these two models share the same critical exponents, which is strong numerical evidence for the existence of a universality class. This universality class is known as the chiral-Heisenberg universality class in terms of the Gross-Neveu model, the celebrated effective model in elementary particle physics.