TOP
 Research
Research
 Research Teams
Research Teams
 Field Theory Research Team
Field Theory Research Team
Field Theory Research Team
Japanese
Team Principal Yasumichi Aoki
 yasumichi.aoki[at]riken.jp (Lab location: Kobe)
yasumichi.aoki[at]riken.jp (Lab location: Kobe)- Please change [at] to @
- 2025
- Unit Leader, Next-Generation HPC Application Development Unit, Next-Generation HPC Infrastructure System Development Division (-present)
- 2018
- Team Leader, Field Theory Research Team (-present)
- 2016
- Associate Professor, Theory Center, High Energy Accelerator Research Organization (KEK)
- 2016
- Fellow, RIKEN BNL Research Center
- 2016
- Researcher, KEK Theory Center
- 2010
- Associate Professor, Center for Theoretical Studies, Nagoya University
- 2006
- Fellow, RIKEN BNL Research Center
- 2003
- Researcher, Physics Department, University of Wuppertal
- 2003
- Postdoctoral Fellow, Department of Physics, Columbia University
- 2000
- Research Associate, RIKEN BNL Research Center
- 1997
- Research Associate, Institute of Physics, University of Tsukuba
- 1997
- PhD, University of Tsukuba
- 1996
- COE Researcher, Center for Computational Physics, University of Tsukuba
- 1996
- Graduate School of Physics, University of Tsukuba completed without degree
Keyword
- Elementary Particle Theory
- Lattice Gauge Theory
- Large Scale Numerical Computations
Research summary
Inferring theoretical predictions from the Standard Model (SM) of elementary particles, which explains most of the existing experimental and observational results of particle physics, often require numerical computation procedures to solve Quantum Chromo Dynamics (QCD) comprised in the SM. These include the predictions of the behavior of particle systems in extreme conditions such as high temperature and/or density, and precision tests of the SM using hadronic reactions as well as investigation of physics beyond the SM.
Numerical simulations with lattice QCD techniques using a realistic set of parameters are becoming feasible. However, many significant questions remain unsolved, which we are addressing by employing lattice methods while preserving as many important symmetries as possible-the symmetries often sacrificed to make the simulations less demanding. In order to use supercomputer Fugaku for such demanding computations, we will develop algorithms, analysis methods, and codes, while performing computation on existing HPC resources. In the first principle computations of the models, we aim to bridge the energy scale layers, and thereby reveal the nature of the evolution of the universe and the mechanism of matter creation in it.
Main research results
Using chiral fermions to analyze high-temperature two-flavor QCD
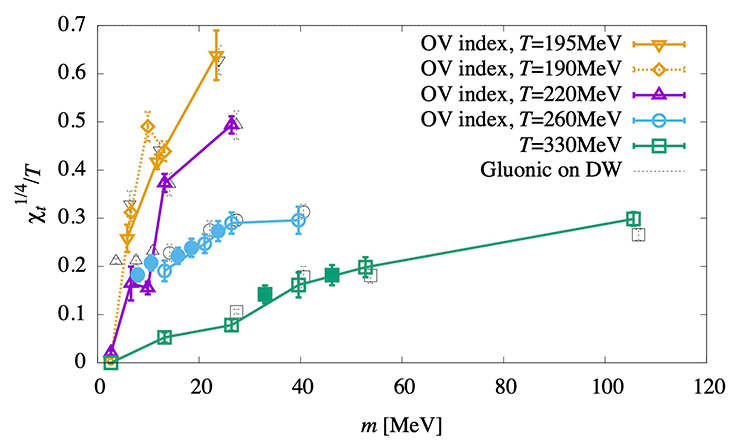
Large-scale numerical computations using lattice chiral fermions are underway to precisely simulate the chiral symmetry and its spontaneous breaking on the computer. Two-flavor QCD is an idealized model of the real-world QCD in a sense that it is made of the up and down quarks, being most essential player of chiral symmetry. It is also regarded as a testbed for the more realistic three-flavor QCD. A theme where chirally symmetry is most relevant is the study of the phase transition where quite a few unresolved problems remain. The figure (from JLQCD collaboration) shows the fourth root of the topological susceptibility for a several different temperatures above the chiral transition temperature. Studying such quantities linking the transition and symmetries like this one is leading to a step-by-step understanding of the phase transition in this system. The study is extended to three-flavor QCD, for which research and development to utilize the supercomputer Fugaku is underway. This R&D would also support the studies for precision tests of the standard model of particle physics and those beyond the standard model.
Representative papers
- S. Aoki, Y. Aoki, G. Cossu, H. Fukaya, S. Hashimoto, T. Kaneko, C. Rohrhofer, K. Suzuki (JLQCD collaboration):
"Study of axial U(1) anomaly at high temperature with lattice chiral fermions"
Phys. Rev. D 103 (2021) 074506. -
C. Rohrhofer, Y. Aoki, L.Ya. Glozman, S. Hashimoto:
"Chiral-spin symmetry of the meson spectral function above Tc"
Phys.Lett. B802 (2020) 135245. -
C. Rohrhofer, Y. Aoki, G. Cossu, H. Fukaya, C. Gattringer, L.Ya. Glozman, S. Hashimoto, C.B. Lang, S. Prelovsek:
"Symmetries of spatial meson correlators in high temperature QCD"
Phys.Rev. D100 (2019) no.1, 014502 -
Eigo Shintani, Yoshinobu Kuramashi (PACS Collaboration):
"Hadronic vacuum polarization contribution to the muon g−2 with 2+1 flavor lattice QCD on a larger than (10 fm)4
lattice at the physical point" Phys.Rev. D100 (2019) no.3, 034517. -
Daisuke Kadoh, Yoshinobu Kuramashi, Yoshifumi Nakamura, Ryo Sakai, Shinji Takeda , Yusuke Yoshimura:
"Tensor network analysis of critical coupling in two dimensional ϕ4 theory"
JHEP 1905 (2019) 184. -
Yoshifumi Nakamura, Hideaki Oba, Shinji Takeda:
"Tensor Renormalization Group Algorithms with a Projective Truncation Method"
Phys.Rev. B99 (2019) no.15, 155101. -
Aoki, Y., Izubuchi, T., Shintani, E., and Soni, A.:
"Improved lattice computation of proton decay matrix elements"
Phys. Rev. D 96, 014506, 1-17. (2017). -
Aoki, Y., et al.: (LatKMI Collaboration)
"Light flavor-singlet scalars and walking signals in Nf = 8 QCD on the lattice"
Phys. Rev. D 96, 014508-1–57. (2017). -
Aoki. Y., et al.: (RBC and UKQCD Collaborations).
"Continuum Limit Physics from 2+1 Flavor Domain Wall QCD"
Phys. Rev. D 83, 074508-1-72. (2011). -
Aoki, Y., Endrodi, G., Fodor, Z., Katz, S., Krieg, S., and Szabo, K.:
"The order of the quantum chromodynamics transition predicted by the standard model of particle physics"
Nature 443, 675-678. (2006).
